رجع إثبات الامتداد اللانهائي للعدد باي إلى عالم الرياضيات يوهان لامبرت، الذي أثبت أن باي هو عدد غير نسبي، ومن ثم فهو عدد لا نهائي حتمًا. (الأعداد غير النسبية أو الأعداد غير الجذرية: هي الأعداد الحقيقية التي لا يمكن كتابتها في صورة كسر اعتيادي).

يحمل الحرف السادس عشر من الأبجدية اليونانية أهميةً كبيرةً في هذا الكون، مثل أهمية الببروني للبيتزا. بدءًا من حساب محيط الصحن الطائر الخاص بك إلى حساب مساحة كوننا. هذا الرمز π قد غير العالم.

هل توجد أي تخمينات حول ماهيته؟

يُحدد محيط كل من الصحن الطائر والكون باستخدام العدد باي

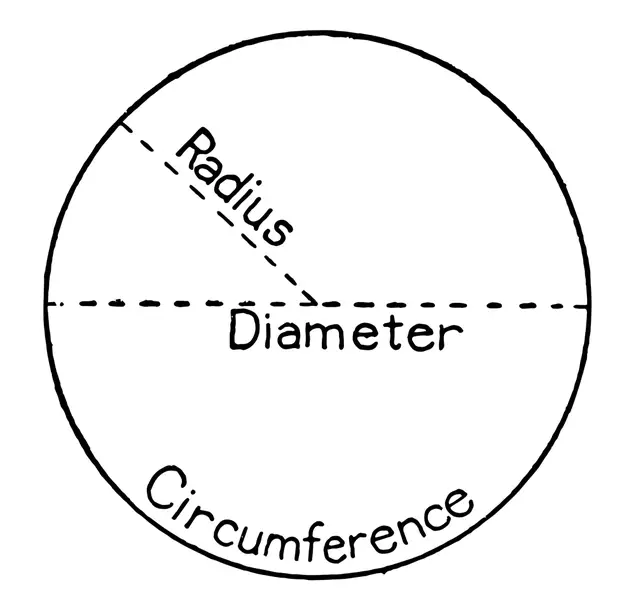
خطان رأسيان متوازيان وخط أفقي واحد، هذا هو العدد π (باي). ربما سمعت عن هذا الرمز أو استخدمته في دروس الرياضيات. محيط الدائرة يساوي 2πr، إذ إن r هو نصف قطر الدائرة.

لكن هل تساءلت سابقًا عن أصل العدد باي؟ وهل لدينا أي دليل على أنه لا نهائي؟ وهل باي هو حقًا ما نعتقد أنه كذلك؟

أصل العدد باي

سيطرت الدوائر على حياتنا منذ القدم. العجلات الخشبية في الماضي، والإطارات المطاطية اليوم.

نظرًا إلى أهمية الدائرة في حياتنا، أربك هذا الاكتشاف الشائع علماء الرياضيات حول العالم، من الهند واليونان إلى مصر والصين. كان قطر الدائرة دائمًا متناسبًا مع محيطها، سواءً كانت الدائرة كبيرة أم صغيرة.

أي إن نسبة محيط الدائرة إلى قطرها تساوي دائمًا قيمة ثابتة، مستقلة عن أبعاد الدائرة. كان عالم الرياضيات الويلزي ويليام جونز أول من أطلق على هذه القيمة الثابتة المتناسبة اسم (باي)، لأنه يمثل الحرف الأول من كلمة (محيط) اليونانية، وبقي الاسم معمولًا به منذ ذلك الحين.

نسبة محيط الدائرة إلى قطرها يساوي القيمة باي

كلا، باي لا يساوي 22/7، وإليكم السبب

تعلمنا في المدرسة الابتدائية أن القيمة باي هي نفسها 22 مقسومًا على 7. ومع ذلك فإن باي شيء أعقد من ذلك بكثير، وهو بالتأكيد ليس 22/7.

إن باي عدد غير نسبي، أي لا يمكن التعبير عنه بنسبة بين عددين صحيحين ليس بينهما عامل مشترك سوى الواحد. لكن لماذا 22/7؟

حسنًا، في الواقع هذا مجرد تقدير تقريبي.

22/7 يساوي 3.142، في حين أن العدد باي هو 3.1415، تختلف القيمة عند الرقم العشري الثالث. تتضمن القيمة التقديرية للعدد باي التي تستخدمها وكالة ناسا في الأغراض العلمية المختلفة 40 رقمًا عشريًا!

تخيل لو أجروا الحسابات باستخدام 22/7! لما تمكن نيل آرمسترونغ وباز ألدرن من الهبوط على القمر!

هل باي عدد لا نهائي؟ ولماذا؟

عندما أثبت عالم الرياضيات يوهان لامبرت أن باي عدد غير نسبي، ثبت أنه عدد لا نهائي في الوقت ذاته، لأن جميع الأعداد غير النسبية هي أعداد لا نهائية.

إن باي هو عدد متسام، أي أنه ليس جذرًا لأي عدد صحيح، فهو ليس عددًا جبريًا، ما يجعله غير نسبي أيضًا. لأن الأعداد النسبية هي أعداد جبرية من الدرجة الأولى، ومن ثم فإذا كان العدد متساميًا، فهو غير نسبي حتمًا.

(الأعداد المتسامية: هي كل عدد حقيقي أو عقدي ليس له حل لأي معادلة حدودية).

ذكرنا سابقًا أنه لا يمكن التعبير عن الأعداد غير النسبية بنسبة بين عددين، ما يجعل امتدادها العشري لا نهائي. يُعَد الامتداد العشري لتلك الأعداد غير منقطع وغير دوري، أي أن العدد لا ينتهي ولا يتكرر أبدًا. لأنه إذا كان لدينا عدد عشري محدود، مثلًا 0.2378، فيمكن تمثيله على أنه 2378/10000 أو 1189/5000.

أي إن هذه الأعداد يمكن التعبير عنها في شكل كسر، فهي أعداد نسبية! إذن فالعدد غير النسبي هو الذي لا يمكن التعبير عنه في شكل كسر، ومن ثم فهو عدد لا نهائي!

لا تخلط بين التعبير اللانهائي لباي وقيمته اللانهائية. باي محدود، في حين أن التعبير عنه لا نهائي. باي له قيمة محدودة بين 3 و4، على وجه التحديد، أكبر من 3.1، وأصغر 3.15.

3<π<4

ومن ثم، فإن باي عدد حقيقي، ولكن نظرًا لأنه غير نسبي، فإن تمثيله العشري غير محدود، لذلك نسميه عددًا لا نهائيًا.

للعدد باي تعبير لا نهائي

كيف نحسب العدد باي ؟

توجد طرق عديدة لحساب باي. يمكنك رسم دائرة، ثم قياس قطرها باستخدام مسطرة وقياس محيطها باستخدام قطعة من خيط. الآن، اقسم محيط الدائرة على قطرها وسوف تحصل على قيمة باي.

تعطينا هذه الطريقة قيمة تقريبية لباي، قريبة من العدد 3. ذكرنا سابقًا أن قيمة باي التي تستخدمها ناسا تتكون من 40 رقمًا عشريًا، ما يطرح سؤالًا: كيف توصلنا إلى معرفة هذه القيمة؟

عمل علماء الرياضيات في جميع أنحاء العالم على مر القرون لتطوير النظريات والصيغ التي تساعدنا على حساب قيمة باي. أصح هذه الطرق هي طرق العلماء:

• غريغوري- ليبنيز.
• نيوتن.
• جون ماشين.
• واليس.
• رامانوجان.

تعد سلسلة غريغوري- ليبنيز ونيوتن وماشين هي الأبسط، أما الوسائل الأخرى فتتضمن مستوى أعلى من الرياضيات.

إحدى الحقائق الممتعة حول باي أنه مرتبط بثابت الجاذبية الأرضية g

إذا استخدمت الآلة الحاسبة لحساب الجذر التربيعي للتسارع الناتج من الجاذبية ستجد التالي:

√g=√9.8=3.1304~3.1415

الجذر التربيعي لثابت الجاذبية الأرضية يساوي تقريبًا قيمة باي! هل هي مصادفة؟

توجد معادلة رياضية تعبر عن العلاقة بين الزمن وطول رقاص الساعة.

T=2π√(L/g)

في حالة رقاص ساعة بطول متر واحد، فإن الزمن يساوي ثانيتين. باعتبار أن T=2 وL=1، نحصل على:

π^2=g

أي إن باي مرتبط بثابت الجاذبية الأرضية!

حياة باي

يُحتفل بالعدد باي يوم 14 مارس من كل عام

كما ترون، يُعَد باي بالفعل جزءًا مؤثرًا جدًا في حياتنا! في الواقع، للعدد باي عيد خاص به، يُحتفل به في 14 مارس من كل عام، إذ يطابق هذا التاريخ 3.14، ويحتل العدد باي مكانةً ضمن أعظم خمسة أعداد في الرياضيات، التي تشمل e وi و0 و1! حتى أن سرعة الحواسيب تُحدد عبر مدى سرعة حساب قيمة باي.

بإمكان الحواسيب الكمومية حساب نحو 2 كوادريليون رقم عشري للعدد باي (كوادريليون: عدد يساوي مليون مليار، أو عشرة مرفوعة إلى القوة 15).

تُعَد حياة العدد باي لا نهائية مثل توسعها العشري. لقد بدأت رحلة باي للتو، وما زال الكثير من الألغاز لم تُكتشف!